Linked Lists in Clojure

Sep 18, 2025

In Clojure, lists are implemented as linked lists by default. Considering its immutable data structures, after reverse-ing a list, we get a completely new list in memory:

(let [original '(1 2 3 4 5)
      reversed (reverse original)]
  (println "Original:" original)
  (println "Reversed:" reversed)
  (println "Same object?" (identical? original reversed))
  (println "Original address:" (System/identityHashCode original))
  (println "Reversed address:" (System/identityHashCode reversed)))

The above code, if run in the REPL, gives the below result on my machine:

Original: (1 2 3 4 5)
Reversed: (5 4 3 2 1)
Same object? false
Original address: 1680485275
Reversed address: 583859661

If the result is what we care about only, this is great. But if we want to manipulate the same nodes of a linked list, as far as my level of Clojure can go, it seems impossible¹. This also makes it fairly difficult (if not impossible) for Leetcode to support Clojure when it comes to linked list problems. Indeed, any problems that expect mutating in-memory data in place will likely cause troubles. Besides, Leetcode sometimes explicitly prohibits this, as Leetcode 25 mentions:

You may not alter the values in the list's nodes, only nodes themselves may be changed.

If a problem doesn't even allow programmers to alter the node values, it will definitely throw errors at any attempt to create a linked list with entirely new nodes.

The rest of this post will nevertheless try to solve 3 Leetcode problems about linked lists, with a simple focus: to get a linked list where the order of nodes is as expected.

Data structure

To better imitate the most common linked lists, we need to define a similar data structure for the nodes of a singly linked list:

(deftype ListNode [value next])

Thus, to make a linked list out of thin air:

(defn make-linked-list
  "Create a head-only singly linked list.  Return the head."
  [value]
  (ListNode. value nil))

We also need to be able to insert a new node at the list head (a.k.a prepend):

;; O(1)
(defn prepend-node [current value]
  (ListNode. value current))

After inserting some nodes, we will want to know the length of the list. Thus:

(defn count-nodes [head]
  (loop [cnt 1
         cur head]
    (if (nil? (.next cur))
      cnt
      (recur (inc cnt) (.next cur)))))

As a dumb human being, I often believe what I see, so God please turn on the light:

(defn print-list
  [head]
  (if (nil? head)
    (println "Empty list")
    (loop [cur  head
           vals [(.value cur)]]
      (if (nil? (.next cur))
        (println (string/join " -> " vals))
        (recur (.next cur) (conj vals (-> cur .next .value)))))))

Now fire up the REPL and try out the below:

(-> (ListNode. 1 (ListNode. 2 (ListNode. 3 (ListNode. 4 (ListNode. 5 nil)))))
    (print-list))
;;=> 1 -> 2 -> 3 -> 4 -> 5

Note, all the above helpers take a ListNode as their first argument.

Leetcode 206: Reverse Linked List

Mutation is forbidden and immutability results in new. Isn't it cool? Instead of node1.next = nil, we prepend node1 to nil, then node2 to the chain of node1 -> nil, and so on:

(defn reverse-list [head]
  (loop [prev nil
         curn head]
    (if (nil? curn)
      prev
      (recur (prepend-node prev (.value curn)) (.next curn)))))

In the REPL, try

(comment
  (-> (ListNode. 1 (ListNode. 2 (ListNode. 3 (ListNode. 4 (ListNode. 5 nil)))))
      (reverse-list)
      (print-list)))
;;=> 5 -> 4 -> 3 -> 2 -> 1

Simple, trivial, isn't it?

Leetcode 92: Reverse List II

This is one of the most awkward things I did with Clojure. I tried hard to not introduce any extra vectors or lists to hold the intermediate list nodes, at the expense of looping over the list one more time.

The first task we need to complete is find the node that lies immediately before the starting left² node. This is because, the problem statement asks us to reverse only the nodes from position left to right (inclusive and left <= right). If we start with the exact node at position left, we will lose the connection with all the previous nodes.

The tricky part for a singly linked list is (almost³) always its head, as it has no previous node. A common workaround is to create a dummy node as the head. Thus, when left = 1, we start with the real (original) head node of the list. Also, when working with a linked list, we can't be too careful due to the possible empty lists (i.e. when head is nil, null, None, etc):

(defn find-prev
  "Position `postion` (1-indexed) is guaranteed to be <= list length.
  This is equivalent to return the previous node of `positoin`.
  If the `position` is 1 (head), return the dummy node."
  [dummy position]
  (if (nil? dummy)
    nil
    (loop [curn dummy
           curp 0]
      (if (= curp (dec position))
        curn
        (recur (.next curn) (inc curp))))))

It just feels criminal if we have find-prev without the corresponding find-next. Agree with me? Hopefully. For a singly linked list, its tail has a perfect mark: it has no next node (of course we are not talking about rings):

(defn find-next
  "`position` is 1-indexed is guaranteed to be <= list length.
  No need for dummy in this search"
  [head position]
  (if (nil? head)
    nil
    (loop [curn head
           curp 1]
      (if (= curp position)
        (.next curn)
        (recur (.next curn) (inc curp))))))

Wait, wait, our toolkit still misses one important widget to find the node at the given position:

(defn find-node
  "`position` (1-indexed) is gunranteeded to be <= list length."
  [head position]
  (if (nil? head)
    nil
    (loop [curn head
           curp 1]
      (if (= curp position)
        curn
        (recur (.next curn) (inc curp))))))

Now that we've got the tools ready, let's get down to work. A few key points:

order of nodes before position left must be retained
order of nodes after position right must be retained
due to the immutability, we have to prepend the nodes in point 1 to the reversed part one by one (done by the inner loop, which runs once, so totally still O(n))

(defn reverse-between
  "Reverse the part between `left` and `right` (1 <= left <= right).
  Return the reversed list."
  [head left right]
  (let [dummy    (prepend-node head "dummy")
        pn       (find-prev dummy left)
        nr       (find-next head right)]
    (loop [prev nr                 ; start prepending onto to the rest
           curn (.next pn)
           cnt  0]
      (if (= cnt (+ 1 (- right left)))
        (loop [oprev pn
               ret prev
               pos (dec left)]
          (if (= pos 0)
            ret
            (recur (find-prev dummy pos)
                   (prepend-node ret (.value oprev))
                   (dec pos))))
        (recur (prepend-node prev (.value curn))
               (.next curn)
               (inc cnt))))))

Note, the prepending is done in reversed order in order to retain the original order. I admit this is not a good solution but it is what I can come up with for now.

Leetcode 25: Reverse Nodes in k-Group

While doing the above Problem 92, it occurred to me that I could not only have a prepend-node helper, but also a prepend-list that inserts an entire linked list before the head of current list:

(defn prepend-list [node lst]
  (loop [n (count-nodes lst)
         head node
         curn (reverse-list lst)]
    (if (zero? n)
      head
      (recur (dec n)
             (prepend-node head (.value curn))
             (.next curn)))))

It is like we push the nodes onto a stack and then pop them one by one when prepending. And this stack-like approach is the key to the solution for the current problem.

Now, for each k nodes, we need to reverse them. With the stack-like behavior in the mind, if we take while building a new list (in Clojure we just have to), isn't it sweet that we will just get a reversed list of the taken-out nodes?

(defn take-n-nodes-reverse
  "Take n nodes starting with head. The resulted linked list is a perfectly
  reversed one. If n is larger than the list length, equivalent to reversing
  the entire list."
  [head n]
  (if (nil? head)
    head
    (loop [lst nil
           curn head
           cnt 1]
      (if (or (nil? (.next curn)) (= cnt n))
        (prepend-node lst (.value curn))
      (recur (prepend-node lst (.value curn))
             (.next curn)
             (inc cnt))))))

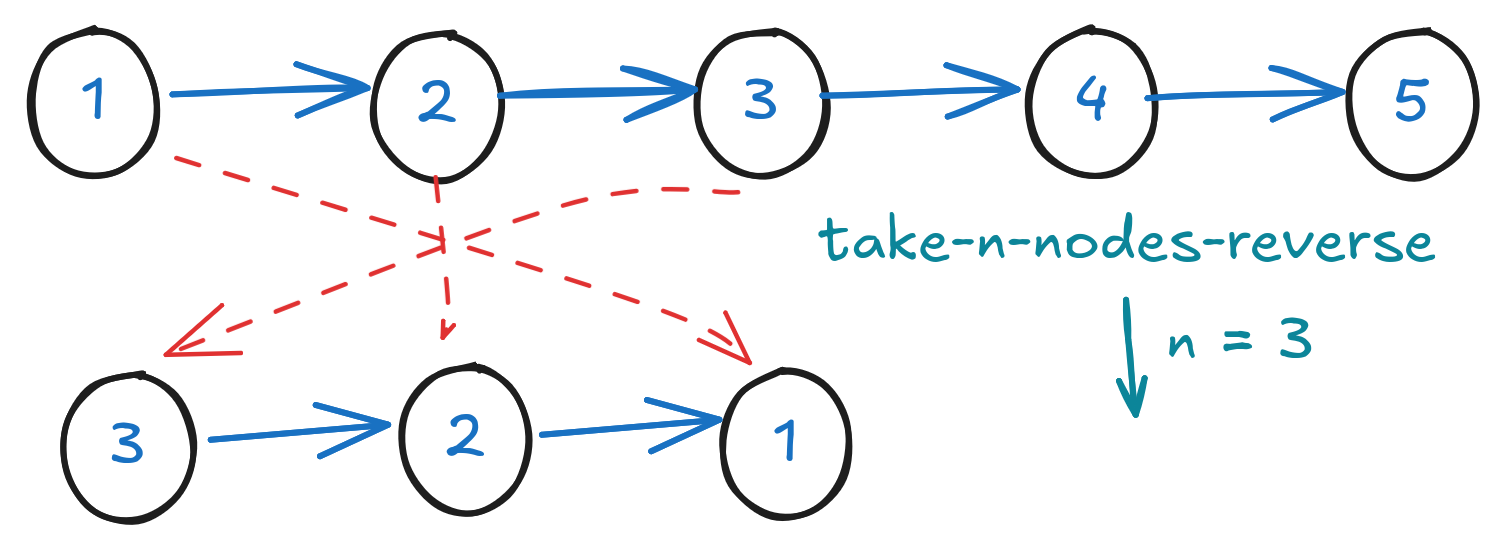
take-n-nodes-reverse

But what if we do need to take n nodes and retain their original order? Push-pop again!

(defn take-n-nodes [head n]
  (if (nil? head)
    nil
    (-> head
      (take-n-nodes-reverse n)
      (reverse-list))))

With these helpers, let's break the problem into the following steps:

find out the number of k-node-groups (list-len / k)
find out if there are any remaining nodes (list-len % k)
use take-n-nodes-reverse to reverse the k-node groups
prepend the reversed groups to the remaining nodes

Sounds good? Actually, the reality is ugly: this is a singly linked list and there is no easy way for quick access to the remaining (tail) nodes. It is however trivial to access the nodes from and/or near the head. Aha, let's reverse the list at the beginning and we will get the k-node groups already reversed. A bonus!

The process looks roughly like below:

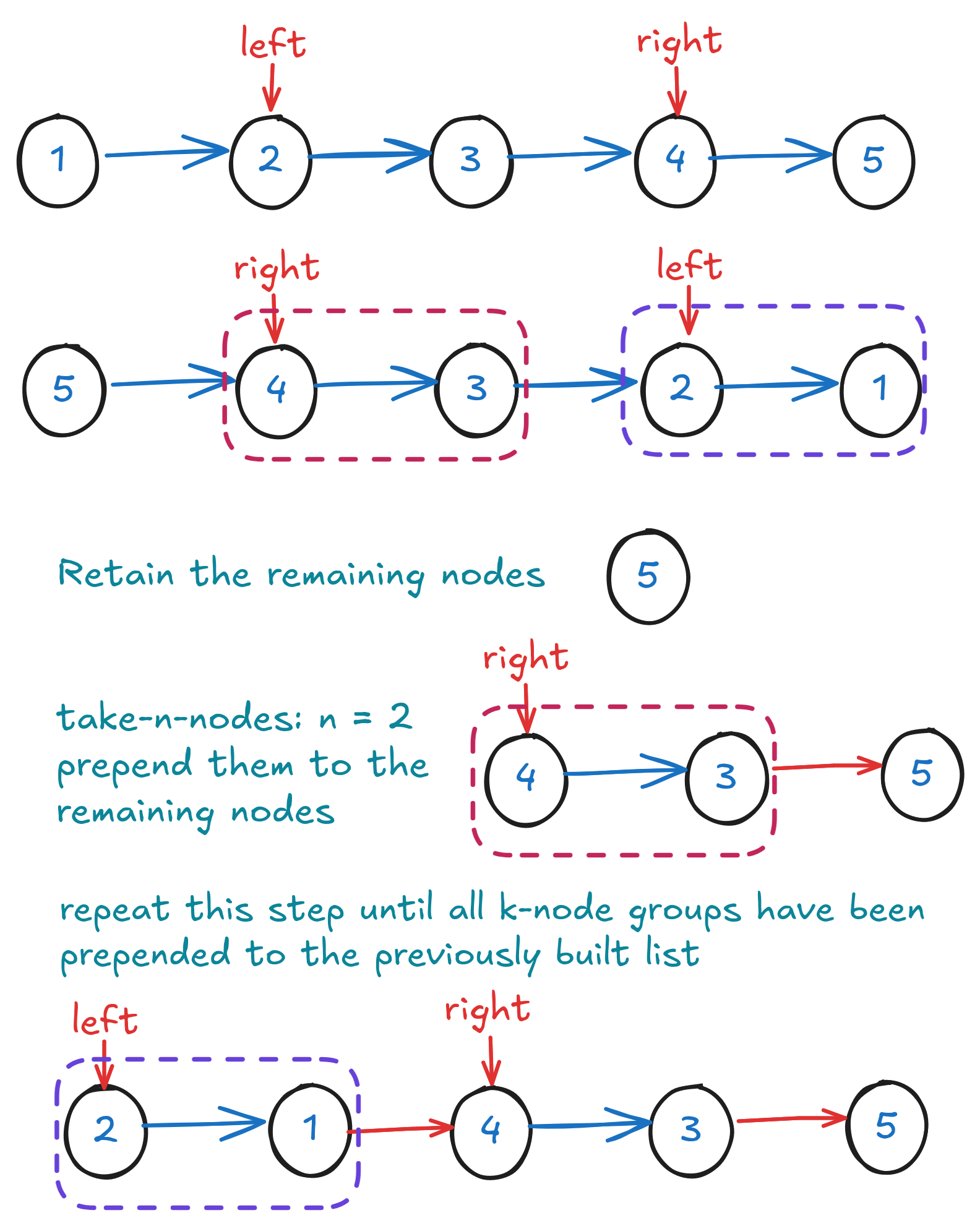
reverse-k-node-groups

(defn reverse-k-group
  [head k]
  (let [l     (count-nodes head)
        m     (rem l k)                    ; number of out-of-k-group nodes
        rhead (reverse-list head)]
    (loop [rcurn  (if (zero? m) rhead (find-next rhead m))
           group  (take-n-nodes rcurn k)
           cnt    0
           mnodes (if (zero? m) nil (take-n-nodes-reverse rhead m))]
      (if (or (nil? rcurn) (= l (+ m cnt)))
        mnodes
        (recur (find-next rcurn k)
               (take-n-nodes (find-next rcurn k) k)
               (+ k cnt)
               (prepend-list mnodes group))))))

The second condition (= l (+ m cnt)) might be redundant but I'm just too lazy to care about it in this case.

Even though it's fun to explore how Clojure handles linked lists, I'd say it also feels a bit awkward. While I'll continue to solve LeetCode-style problems with Clojure from time to time, I doubt I'll delve deeper into linked lists using the language.